Linear Regression with python and Scikit-learn

Scikit-learn is a wonderful software package for performing various computations in the field of machine learning. Let us consider the calculation of the linear regression.

An equation Simple Linear Regression (SLR) have a view:

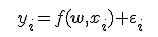
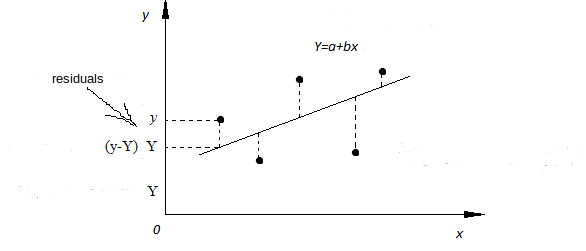
SLR models also include the errors in the data or residuals (y - Y). Residuals are basically the differences between the true value of y and the predicted/estimated value of Y. In a regression model we are trying to minimize these errors, can say, that we are trying to find the “line of best fit” — the regression line from the errors would be minimal.

 

Let's go to the code

All the code for this article can be found here.

for test data we take a file test_dataset.csv, which describes the relationship between work experience and annual salary

import necessary libraries:

import pandas as pd  
import numpy as np  
import matplotlib.pyplot as pl

load dataset:

dataset = pd.read_csv('test_dataset.csv')
dataset.shape

dataset.head()

show the first 5 records from our dataset, the output will be like this:

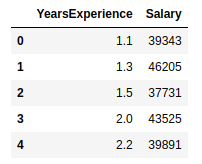
dataset.describe()

show statistical details of the dataset

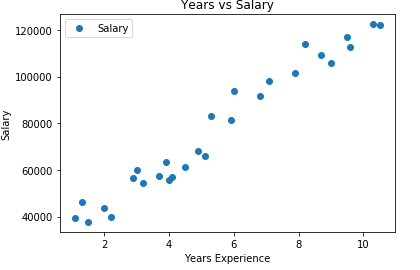
dataset.plot(x='YearsExperience', y='Salary', style='o')  
plt.title('Years vs Salary')  
plt.xlabel('Years Experience')  
plt.ylabel('Salary')  
plt.show()

printing our dataset, the output will be such:

take values without headings:

X = dataset.iloc[:, :-1].values  
y = dataset.iloc[:, 1].values

distribute 80% of the data to training set while 20% of the data to test set:

from sklearn.model_selection import train_test_split  
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0) 

train model:

from sklearn.linear_model import LinearRegression  
regressor = LinearRegression()  
regressor.fit(X_train, y_train)

make prediction:

y_pred = regressor.predict(X_test)

and compare prediction and actual value:

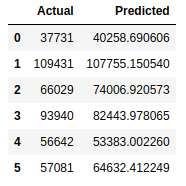
df = pd.DataFrame({'Actual': y_test, 'Predicted': y_pred})  
df

Now we can look such table, which contains the actual values and our predictions

calculate the values:

Mean absolute error

Mean squared error

Root-mean-square deviation

from sklearn import metrics  
print('Mean Absolute Error:', metrics.mean_absolute_error(y_test, y_pred))  
print('Mean Squared Error:', metrics.mean_squared_error(y_test, y_pred))  
print('Root Mean Squared Error:', np.sqrt(metrics.mean_squared_error(y_test, y_pred)))

There is a wonderful article that describes the differences in errors.

Print result

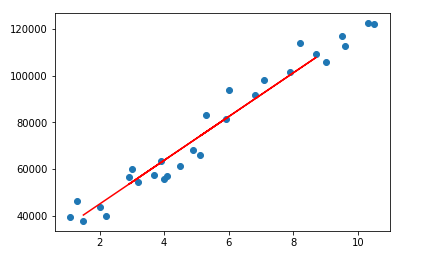
plt.scatter(X, y)
plt.plot(X_test, y_pred, color='red')
plt.show()

Multiple Linear Regression

Model for multiple linear regression is created similar to simple linear regression. The code you can find here